두뇌는 최강의 실험실: 생각을 더 잘 하는 방법
상트페테르부르크의 역설로 알려진 도박 게임이 있다. 참가자는 동전을 앞면이 나올 때까지 계속 던진다. 앞면이 나오면 그때까지 던진 횟수가 N이라고 할 때, \(2 ^ N\) 만큼 상금을 받고 게임이 끝난다. 예를 들어, 던지자마자 앞면이 나오면 \(2 ^ 1 = 2\)원을 받는다. 두 번만에 앞면이 나오면 4원, 세 번이라면 8원이다. 이 도박을 단 한 판만 한다고 했을 때, 여러분은 참가비로 얼마까지 지불할 의향이 있는가?
계산해보면 알겠지만 이 도박의 상금 기댓값은 무한대이다.
\[2^1 \cdot \frac{1}{2^1} + 2^2 \cdot \frac{1}{2^2} + 2^3 \cdot \frac{1}{2^3} + ...\]설마 기댓값이 무한이니 이 게임 한 판에 전재산을 걸겠다는 사람은 없겠지? 진짜 질문은 바로 이것이다. 수학적으로는 합리적인(?) 결정인데, 왜 전재산을 거는 게 말도 안 된다고 “느껴지는가”?
현실에서는 대박이 터질 때까지 무한하게 도박을 할 수 없기 때문이라는 설명도 있고, 금액은 무한대로 커져도 효용은 한계에 이르기 때문(“한계효용 체감의 법칙”)이라는 베르누이의 설명도 있다는데…
이 도박에 여러 번 참가했을 때, 획득하는 상금의 분포는 어떤 모양일까? 1천만 번 했을 때, 상금은 X축, 그 상금을 얻은 횟수, 즉 빈도를 Y축에 그렸다. 왼쪽 그래프는 원래 스케일이고, 오른쪽은 Y축을 로그 스케일로 변환했다. 참여한 게임의 대부분에서는 낮은 상금만 받는다는 것을 알 수 있다.
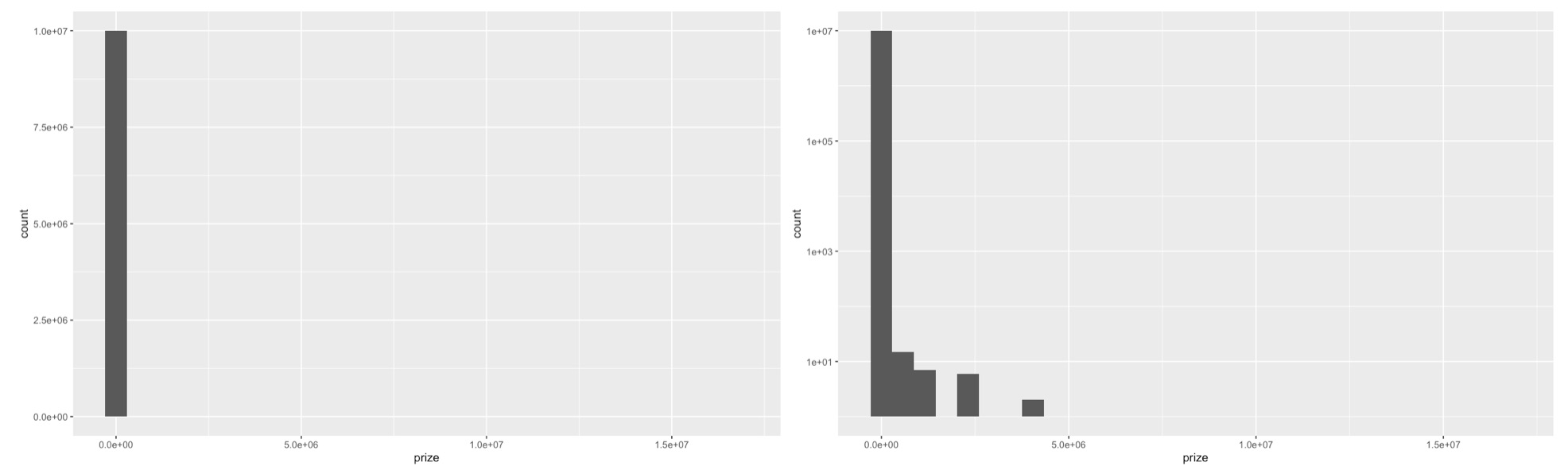
구체적인 통계 수치를 보자. 1천만 번 실험에서 얻은 상금의 기댓값과 분위수이다.
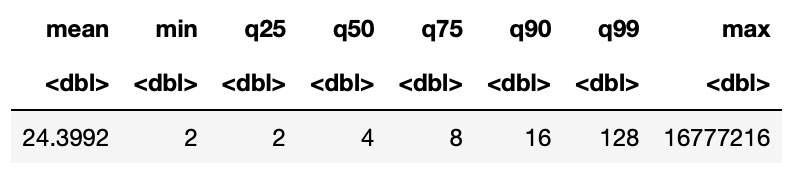
- 1천만 번 했을 때의 상금 기댓값은? 24.4에 불과하다. 이론적인 값은 무한대지만, 가령 100번 연속으로 뒷면이 나올 확률은 너무나도 낮기 때문에 1천만 번을 해도 그런 사건은 발생하지 않았다.
- 분위수(q25, …, q99)는 어떤가. 100명 중에 2번째로 운이 좋은 사람이라도 128원밖에 못 받고, 운이 중간인 사람은 고작 4원을 받는다.
우리의 직관은 기댓값과 일치하지 않으며 그 사건이 발생할 확률 같은 요소를 암묵적으로 반영하고 있을 것이라는 생각을 하게 된다. 거꾸로 생각하면, 직관적으로는 불리하게 느껴지지만 기댓값 기준에서는 합리적인 게임도 있을 수 있다는 뜻이다.
다음으로, 확률의 알쏭달쏭함을 보여주는 유명한 문제인 몬티홀 딜레마를 보자. 지금 내 앞에는 3개의 문이 있고, 그중 하나에만 상금이 있다. 내가 문 하나를 선택하면, 사회자가 나머지 2개 중에서 상금이 없는 문 하나를 열어서 보여준다. 나는 원래의 선택을 고수할 수도 있고, 바꿀 수도 있다. 어떻게 해야 할까?
이제는 많이 알려진 문제이고, 정답 해설도 나와 있다. 그런데도 왜 최선의 선택이 자연스럽고 당연하게 느껴지지 않을까? 매번 숫자를 적어서 풀어볼 수도 없는데, 어떻게 하면 비슷한 상황에 처했을 때 직관적으로 좋은 결정을 할 수 있을까?
내가 들은 가장 직관적인 설명은 다음과 같다. 문의 개수를 3개에서 100개로 바꾼다. 문 하나를 선택하면 사회자가 나머지 99개 중 98개의 비어있는 문을 열어서 보여준다. 이제는 느낌이 어떤가? 아직도 선택이 망설여지는가? 문제의 설정을 극단적으로 바꿈으로써 처음에는 모호했던 사회자의 행동이 가지는 가치가 명확해졌다.
이제 숫자의 세계를 떠나 물리적인 현실로 돌아오자. 세 번째 질문이 준비되어 있다. 무거운 물체와 가벼운 물체를 동시에 떨어뜨리면 무엇이 먼저 땅에 떨어질까? 물론 이미 답을 알고 있을 것이다. 그런데 물리학 지식이나 실험 없이도 같은 결과를 도출할 수 있을까?
수세기 전에 살았던 갈릴레이는 가능했다. 무거운 물건이 더 빨리 떨어진다고 가정해보자. 무거운 물건과 가벼운 물건을 단단하게 연결해서 떨어뜨리면 무슨 일이 벌어질까? 무거운 물건은 가벼운 것이 더 빨리 떨어지도록 당기고, 반대로 가벼운 물건은 무거운 것을 당겨서 혼자 떨어질 때보다 속도를 늦출 것이다. 따라서 연결된 두 물체는 각각이 혼자 떨어졌을 때의 중간 정도의 속도로 떨어져야 한다. 하지만, 한편으로는 두 물건을 단단히 연결했으므로 원래보다 더 무거워졌다. 처음 가정에 따르면 더 빨리 떨어져야 한다. 모순이 발생했다. 그 원인은? 갈릴레이는 이런 사고실험을 통해 진짜 실험 없이도 결과를 예측하거나 설명할 수 있었다.
위의 몇 가지 사례에서 진실과 직관의 괴리를 느껴보았고, 발상의 전환이나 추론을 통해 더 잘 생각하는 방법을 살펴보았다. 이 내용은 모두 『두뇌는 최강의 실험실』 책에서 가져온 것이다. 저자는 역사적으로 유명한 사고실험을 소개하며, 그것이 나온 역사적인 맥락과 의미를 너무 깊이에 짓눌리지 않을 수준에서 설명해준다. 이런 생각의 도구는 유용하다. 직관을 날카롭게 갈아주기도 하고, 비슷한 상황에서 약간의 설정 변경에 따라 달라지는 느낌과 결론을 보면서 자신의 생각에 대해서도 다시 한 번 생각해보게 된다. (어쩌면 디버깅까지도?) 흥미로운 사고실험의 세계로 안내를 바란다면 이 책을 읽어봐도 좋겠다.