Active Learning: 무엇을 먼저 배울 것인가
어떤 데이터를 먼저 레이블링해서 알고리즘이 학습하게 할 것인지가 액티브 러닝(Active Learning, 번역하면 능동학습?)의 핵심 질문이다. 우리의 경험에 비추어보자. 자신을 발전시키고 싶을 때, 스스로에게 무엇을 먼저 배우게 할 것인가?
첫 번째 방법은 알쏭달쏭한 것부터 물어보는 것이다. “Q1 문제에 대한 답은 A1이라고 생각하고 정답을 확신해. 그런데 Q2에 대한 답은 A2같기는 한데 자신은 없어.”라는 상황에서 무엇을 물어야 할지는 자명하다. 이런 방식을 Uncertainty Sampling이라고 하고, 불확실성을 정량화하기 위해 아래의 방식들이 제안되었다.
- argmin P(y1|x): 답에 대한 확신이 가장 약한 문제 x를 찾는다. (y1은 x에 대해서 모델이 답이라고 예측한 레이블)
- argmin P(y1|x) - P(y2|x): 가장 답이라고 생각하는 항목을 2개 뽑는다. (확신하는 순서대로 y1, y2) 이 두 개 사이에서 헷갈리는 정도가 큰 문제 x를 찾는다.
- 엔트로피: 선택가능한 모든 답에 대해서 정답이라고 생각하는 확률을 매긴 뒤, 이 분포가 많이 퍼져있는 x를 찾는다.
이와 비슷한 듯 다른 방법이 있다. 사람들이 상반된 조언을 하는 문제를 찾는 것이다. 예컨대 다이어트를 하려고 하니 누구는 이 음식을 먹으라고 하고 누구는 먹지 말라고 하는 상황이다. 위원회에서 의견을 한 표씩 던진 뒤 결과가 가장 불일치하는 의제를 찾는다고 해서 Query by Committee라고 부른다. 똑같은 데이터가 주어지더라도 서로 다른 모델(e.g. Decision Tree, Naive Bayes 등)로 학습하면 예측이 엇갈리는 케이스가 나온다. 그 케이스에 대한 정확한 답을 알면 모델의 정확도 개선에 도움이 될 것이다. 불일치를 정량화하는 방법은 Uncertainty Sampling과 비슷하다. 위원들에게서 받은 표의 비율을 확률로 보고 엔트로피를 계산하거나 위원회 전체의 의견과 각 위원의 의견의 차이(KL divergence)의 평균을 구한다.
보다 전략적으로 접근할 수도 있다. 내가 만약 답을 알게 된다면 기존에 갖고 있던 생각을 가장 많이 바꿀 수 있을 문제를 택하는 아이디어는 어떤가? 이른바 Expected Model Change 방식이다. 알아도 그만 몰라도 그만인 내용만 공부하는 것보다 효율적인 학습을 가능케 하지만 자칫하면 신기하거나 특이한 문제 때문에 길을 잃을 위험이 있다. 만약 초자연적인 현상의 비밀을 알게 된다면 나의 가치관은 엄청나게 바뀌겠지만 답을 발견도 못하고 신기루를 좇으며 인생을 허비할 수도 있다. 물론 극단적인 예이기는 한데, 실제로 피처(Feature) 값이 잘못 스케일링된 경우에 데이터의 정보성이 과대평가될 수 있으므로 정규화(Regularization)가 필요하다고 한다.
또 다른 접근으로 Expected Error Reduction이 있다. 내가 앞으로 만나게 될 문제들에서 시행착오를 줄여줄 수 있는 문제를 먼저 풀겠다는 것이다. 교과서의 연습 문제 같은 느낌이다. 아직 접해보지 않은 문제에 대한 예측 오류(Expected Error)를 어떻게 계산하는지 궁금했는데, 문제 풀(Pool)에서 문제를 하나씩 빼서 기존 데이터와 그 문제를 이용해서 학습했을 때 풀의 나머지 문제들에 대한 예측의 엔트로피를 구하는 방식을 제안한 연구 논문이 있었다. 그 엔트로피가 최소가 되는 문제부터 풀면 된다. 이 방식의 단점은 그런 문제를 찾는 일 자체에 무시못할 정도의 시간이 든다는 점이다. 무엇을 공부할지 고민하느라고 진짜 공부할 시간을 빼앗기면 안 되니까 균형을 잘 잡아야 한다.
기계학습 연구자들이 액티브 러닝이라고 부르는 분야에는 사실 또 다른 이름이 있다. 학습할 문제의 레이블링을 요청하는 일은 달리 말하면 실험을 수행해서 데이터를 얻는 과정이다. 예를 들어, 여러 종류의 비료로 농사를 지어 수확량을 비교하고자 한다면 이 실험의 비용은 레이블을 물어보는 것과는 차원이 다르다. 통계학에서는 일찌감치 이 주제에 실험계획(Experimental Design)이라는 이름을 붙여놓고 어떻게 최적화할지 연구해왔다.
분류 문제는 아니지만 선형 회귀분석 예제를 통해서 구체적으로 살펴보자. 학습용 데이터가 n개 있으며, 각 데이터는 2개의 피처를 가지고 있다고 가정한다. X는 n개의 행, 3개의 열(피처 2개 + Intercept)을 가진 매트릭스이다. Y는 n개 데이터의 타겟값을 가진 벡터이다. \(Y = X \beta\)를 적합(Fit)할 것이다. 가중치 \(\beta\)를 최대우도법(MLE)으로 추정하면,
\[\hat{\beta} = (X^{T}X)^{-1}X^{T}Y\]이렇게 구한 \(\hat{\beta_{j}}\)은 진짜(Unknown Truth) \(\beta_{j}\)의 추정값이다. \(\beta_{j}\)의 신뢰구간(Confidence Interval)은 다음과 같다.
\[\hat{\beta_{j}} \pm (\alpha \times \hat{se}(\hat{\beta_{j}}))\]위 식에서 se는 Standard Error를 의미하며, 추정한 파라미터의 표준 편차이다. 그럼 se는 어떻게 구하는가?
\(\hat{se}^{2}(\hat{\beta_{j}})\)은 \(\sigma^{2} \times (X^{T}X)^{-1}\)의 j번째 Diagonal Element이다. \(\sigma\)는?
\[\sigma^2 = \frac{1}{n-k} \sum_{i=1}^{n}(X_{i} \hat{b} - Y_{i})^{2}\]n과 k는 각각 학습에 사용된 데이터와 파라미터의 개수이다. (All of Statistics, 217p)
이제 원래의 관심사로 돌아온다. 우리의 목표는 적은 레이블/실험으로 \(\beta\)를 최대한 정확하게 추정하는 것이다. \(\beta\) 추정치의 신뢰도를 높이려면 \(se(\hat{\beta})\)를 낮춰야 한다. se는 \((X^{T}X)^{-1}\)가 결정하므로, 가능한 실험횟수가 m번이라면, 우리는 실험을 최적화하기 위해 전체 Xi…Xn 중에서 \(se(\hat{\beta}) = (X^{T}X)^{-1}\)을 최소화하는 m개의 X를 찾아야 한다. 여기서 \(\hat{\beta}\)은 3개의 값을 가지는 벡터이고, 인터셉트 b0, x1 피처의 가중치 b1, x2 피처의 가중치 b2로 구성되어 있다. 순위를 정하기 위해 벡터를 하나의 숫자로 만들어야 하는데, \(se(b_{0}) + se(b_{1}) + se(b_{2})\), 즉 \((X^{T}X)^{-1}\)의 trace를 최소화하는 방식을 A-optimality라고 부른다. 이외에도 행렬식(Determinant)를 최소화하는 D-optimality, 최대 고윳값(Eigenvalue)를 최소화하는 E-optimality 등 여러가지가 있다.
이상의 내용을 Iris 데이터로 실습해보았다. Sepal.Width와 품종(setosa인가, versicolor인가)을 입력받아서 Sepal.Length를 예측하는 선형회귀 모델을 만들어야 하는 상황에서 실험계획법은 어떤 답을 줄 것인가? 전체 150개 데이터와 그중에서 A-optimality가 점지해준 샘플 10개(큰 동그라미)를 그래프로 그렸다.
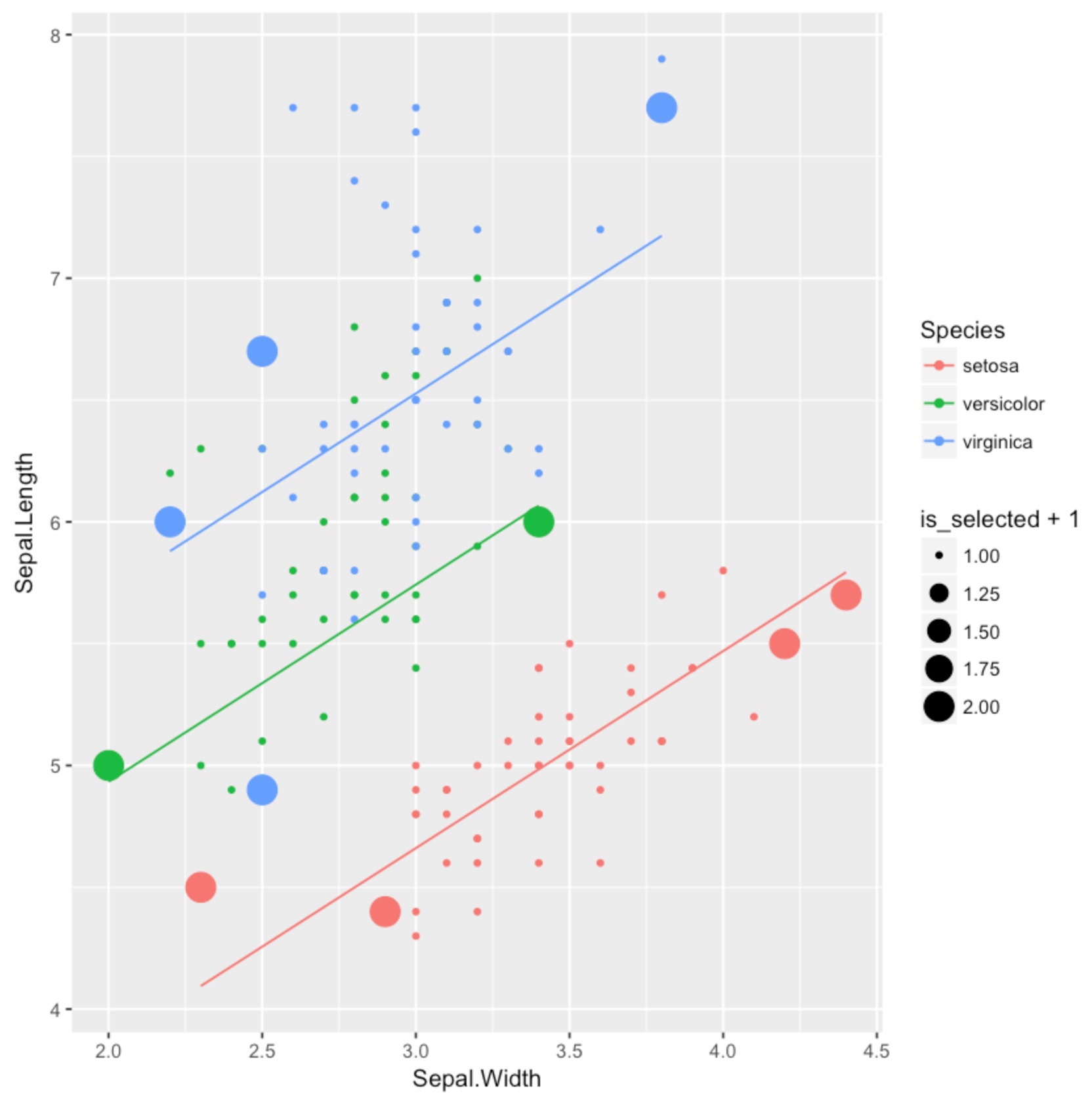
그리고 직선은 그 10개의 샘플만으로 학습한 모형이다.
참고 자료
- Active Learning Literature Survey, Burr Settles, 2010 (액티브 러닝 관련 이슈와 연구를 잘 소개하는 서베이 논문)
- Active Learning via Transductive Experimental Design, Kai Yu et al, 2006
- All of Statistics: A Concise Course in Statistical Inference, Larry Wasserman, 2004