인지하는 확률과 실제 확률의 관계
우리가 체감하는 확률 혹은 상대적 빈도는 실제와 다르다. 인지하는 과정에서 왜곡이 발생하기 때문이다. 그렇다면 왜곡은 임의적으로 발생하는가 아니면 어떤 규칙을 따르는가. 이 질문에 흥미로운 답을 제시하는 글을 읽었다.
많은 연구에서 보고된 바에 따르면, 왜곡된 확률(Probability Distortion)과 진짜 확률에 어떤 함수 하나를 취해서 그래프를 그리면 둘 사이에 선형적인 관계가 나온다고 한다. 이런 현상이 특정한 문제에 국한되지 않고 다양한 경우에서 공통적으로 관찰된다고 해서 흥미를 더한다. 예를 들어, 사람들에게 영어 텍스트에서 알파벳 문자의 등장 횟수나 미국의 사망 원인(e.g. 홍수, 살인, 자동차 사고 등) 비율을 추정하게 한 연구가 있었다. 이런 상대적 빈도는 확률로 볼 수 있고 통계 데이터도 구축되어 있으므로 우리가 인지하는 확률이 얼마나 실제와 다른지 쉽게 비교할 수 있다. 인용한 그래프를 보면 발생 확률이 작은 이벤트는 실제보다 높게 추정하고, 반대로 흔한 이벤트는 더 낮게 추정하는 경향이 보인다. 하지만 딱 봐도 선형 관계는 아니다. (그래프는 원문에 다 있다.)
실제 확률과 왜곡 확률의 관계를 선형으로 바꿔주는 함수는 과연 무엇일까? 바로 Log Odds다. 함수의 수식과 모양은 아래와 같다.
\[Lo(p) = log(\frac{p}{1-p})\]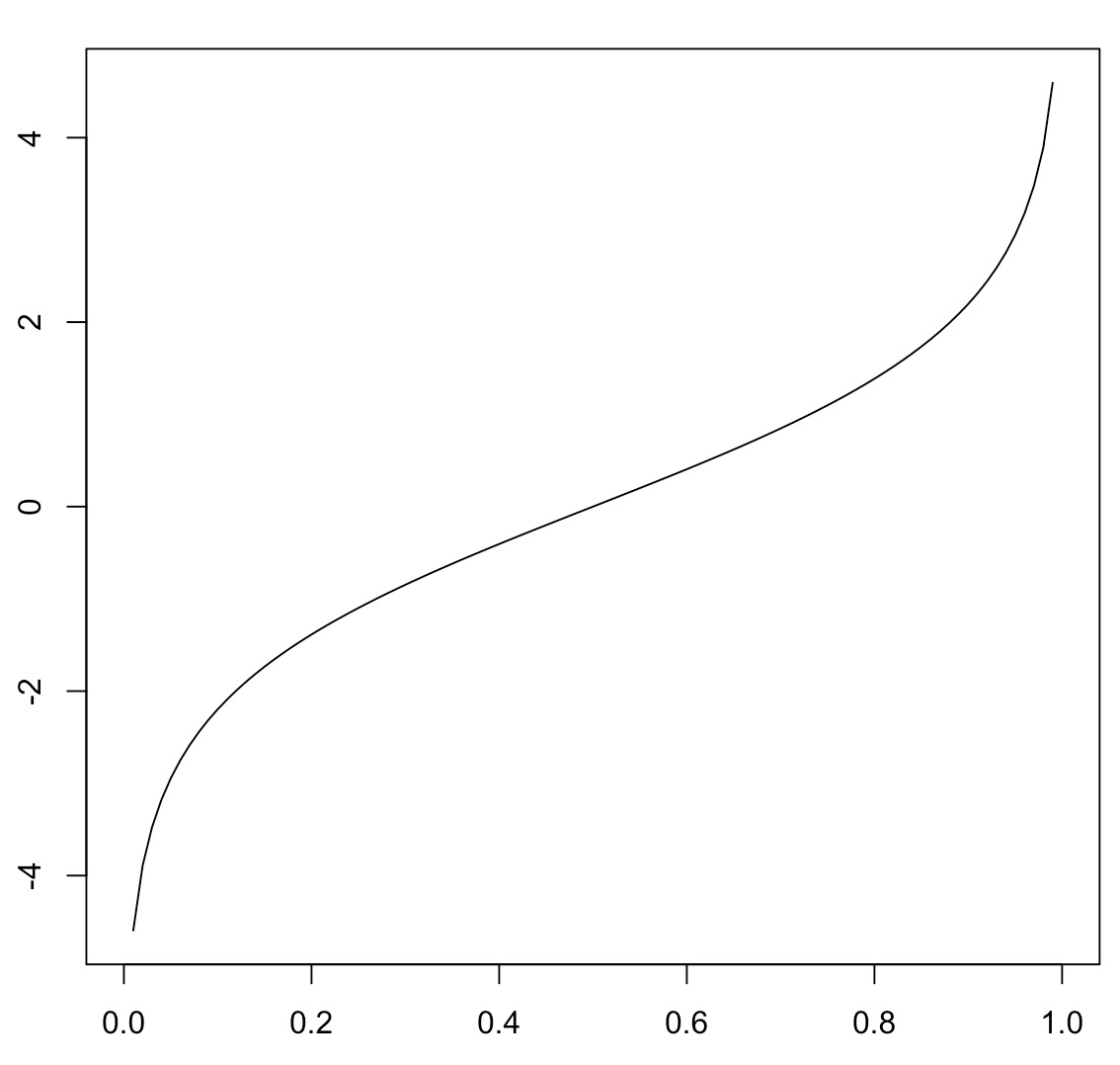
두 확률의 관계를 저자들은 아래의 LLO(Linear in Log Odds) 식을 써서 표현한다.
\[Lo(\pi(p)) = \gamma \times Lo(p) + (1-\gamma) \times Lo(p_{0})\]p는 실제 확률을 의미하고, π(p)는 왜곡된 확률이다. γ는 기울기로서, 위의 상대적 빈도 예제처럼 (확률이 낮은 것은 높게, 높은 것은 낮게) 추정을 하는 경우 1보다 작은 값을 가질 것이다. \(p_0\)는 p = π(p)인 점이고, 크로스오버 포인트(Crossover Point, 왜곡되었던 확률이 실제와 교차하는 지점)라고 부른다. Log Odds의 세상에서 선형적인 관계를 갖기는 하지만 문제에 따라서 파라미터 γ와 \(p_0\)의 값은 달라질 수 있다.
Log Odds의 마법은 상대적 빈도 문제만이 아니라 주관적인 믿음의 확률에서도 계속된다. 객관식 문제(e.g. 붓다와 아리스토텔레스 중에 누가 먼저 태어났는가?)를 내면서 답을 확신하는 정도(Confidence Rating)도 같이 물었다. 그러면 확신하는 정도 별로 실제 정답이었던 확률을 구할 수 있으니 두 확률을 비교할 수 있다. 또 다른 연구에서는 실험 참여자에게 농구 슛을 하기 전에 성공할 것 같은지를 숫자로 평가하게 한 뒤 실제 성공 여부와 비교했다. 예상한 것처럼 두 경우 모두 Log Odds를 취하자 선형 그래프가 나타났다. 그런데 앞에서 나온 빈도 문제와 다른점이 있었다. 이번에는 성공 확률이 높을 때는 실제보다 더 높게 평가하고, 낮을 때는 더 낮게 평가를 했다. LLO의 기울기 γ가 더 가파르게 변한 것이다. 이런 현상에는 hard-easy effect라는 이름도 붙어 있다.
이외에도 도박에서 이길 확률을 추정하는 문제나 일렬로 나열된 하얀점과 검은점들을 본 뒤 색깔의 비율을 맞히는 지각 문제에서도 같은 패턴이 관찰되었다. 다만 문제 종류와 상황에 따라서 파라미터, 즉 LLO의 기울기와 크로스오버 포인트가 달랐다. 이제 관심은 이 파라미터에 영향을 끼치는 요소는 무엇인가로 옮겨간다. 답을 밝혀내기 위해 저자들이 실시한 실험과 해석, 이런 인지 왜곡이 발생하는 메커니즘을 설명하기 위해 기존에 제안된 모델을 개괄한 내용이 원문에 있으니 관심있는 분들은 읽어보면 좋을 것 같다. 저자들의 실험에서 Sample Numerosity가 클수록 기울기 γ가 작아지는 경향이 있고, 확신도(Confidence Rating)를 묻는 실험은 샘플이 매우 작은 상황이라고 볼 수 있으니 그때 γ가 큰 것이 뭔가 관련이 있지 않을까 라는 얘기를 하는데, 긴가민가 하면서도 흥미로운 부분이 있었다.
PS1. 원글에서 인용하는 연구들이 적어도 1950년대 이후의 논문이기는 한데, 처음으로 사람의 확신도와 실제 확률의 관계를 밝혀낸 때는 1885년이라고 한다. (아래의 연구도 언급은 하고 있다.)
피실험자가 판정을 내릴 때마다 맞는다고 믿은 확신도 C까지 연구 내내 기록지에 남겼다. 확신도 C는 가장 낮은 값이 0이고, 1, 2를 거쳐 가장 큰 값이 3이었다. 두 사람이 파악한 결과, 추측이 맞는 확률 p가 커질수록 확신도도 log(p/(1-p))의 배수에 가까이 커졌다. 로그 오즈는 두 사람이 옳았다는 것을 보여주었다. 두 사람이 이에 앞서 맞고 틀림을 인지하는 능력이 로그 오즈 척도에 선형으로 근사한다는 증거를 찾아냈기 때문이다., 『통계학을 떠받치는 일곱기둥 이야기』 163p
PS2. 나는 음악을 들을 때 곡 순서를 랜덤으로 하는 편이다. 그런데도 이상하게 어떤 노래는 정말 오랜만에 듣는 것 같고, 어떤 노래는 ‘왜 이렇게 자주 나오지’라는 생각이 든다. 어쩌면 그 이유가 이 글에서 얘기한 왜곡 때문인지도 모르겠다. 좋아하는 노래는 실제보다 안 나온다고 느끼거나, 오래전부터 알았던 익숙한 노래는 실제보다 더 자주 나온다고 느끼거나. 만약 그렇다면 정확한 확률보다 체감이 더 중요한 상황에서는 인지적 왜곡을 역으로 이용하면 좋지 않을까? 즉, 정확한 랜덤을 구현하기보다 사용자가 체감하는 확률이 랜덤으로 느껴지도록 알고리즘을 만드는 것이다.