Anand Rajaraman과 스탠포드 대학교의 Jeff Ullman 교수 (맞다, Advising students for success를 쓴 그 Ullman 교수다)가 공저한 Mining of Massive Datasets 책을 사려고 하면 7만 원이 넘지만 PDF 파일은 여기에서 무료로 다운받을 수 있다. 이 책 4장의 제목은 Mining Data Streams이다. 밀물처럼 쓸려오는 거대한 데이터의 흐름을 효율적으로 처리하는 기법들을 소개하고 있다. 이 글에서는 대충 어떤 문제들을 해결하려고 하는지만 정리해보자. 바탕에 깔린 전략은 해쉬(Hash) 함수를 이용해서 근삿값을 찾겠다는(Approximate) 것이다. 스트림 데이터의 예로 검색엔진에 유입되는 쿼리를 생각해보자.

t1  t2  t3  t4  t5  t6  t7  ...  tn
q1  q2  q1  q3  q2  q2  q3  ...  qn

t1 ~ tn은 각 쿼리가 들어온 타임스탬프이고, 그 아래의 q는 그 타이밍에 들어온 쿼리이다. 그리고 각 쿼리의 유입수를 c로 표기한다. 위의 예에서, 유니크한 쿼리의 개수는 3개이며, q1과 q3는 각각 2번, q2는 3번 검색되었으므로, c1은 2, c2는 3, c3은 1이다.

1. Sampling

첫 번째 문제는 샘플링이다. 정말로 엄청나게 많은 데이터가 몰려와서 전부 저장하는 게 불가능하다면, 어쩔 수 없이 일부만 샘플링해서 처리/저장해야 한다. 그때 단순히 랜덤으로 샘플을 고르기보다는 특정한 키(Key)를 정해서 그 키에 해쉬함수를 적용한 결과에 따라 샘플링을 하는 게 좋다. 쿼리 스트림 예에서라면, 타임스탬프 t보다는 쿼리 q를 키로 쓰는 게 낫고, 또 그보다 나은 키가 있다.

2. Filtering

두 번째 문제는 필터링이다. 만약 유입된 쿼리 중에서, 내가 미리 정해놓은 셋에 속하는 것만 남기고 싶다면 어떻게 해야 할까? 참고로, 미리 찜해놓은 쿼리의 개수는 10억 개 정도 된다. 이럴 때 쓸 만한 방법으로 Bloom Filtering을 소개하고 있다. 해쉬값을 계산해서 비트에 저장하는 방법이다.

3. Counting Distinct Elements

타임스탬프 t1부터 t100000000까지, 즉 1억 개의 유입 쿼리 중에서 유니크한 쿼리의 개수를 알고 싶다면? 정확한 수치를 계산하려면 모든 쿼리를 다 저장해야 하므로 공간복잡도가 매우 커진다. 그러나 대략적인 추정으로도 충분하다면 Flajolet-Martin 알고리즘을 이용할 수 있다. 이 또한 해쉬함수를 활용해서 근사하는 방식이다.

4. Estimating Moments

이 책에서는 Second Moment를 c1^2 + c2^2 + … + cn^2로 정의했고, 이 값은 쿼리의 검색횟수 분포가 얼마나 쏠렸있는지를 나타낸다. 각 쿼리의 유입수를 모두 알아야 하기 때문에 Second Moment 계산은 비용이 많이 드는 작업이다. 이럴 땐 쿼리 일부의 유입수만 가지고 전체의 모멘트를 추정하는 Alon-Matias-Szegedy 알고리즘을 고려해볼 만하다.

5. Counting in a Window

지금까지는 각 타임스탬프마다 유입 쿼리가 찍힌 스트림을 가지고 얘기했다. 이제 예를 바꿔보자. 쿼리별로 스트림이 따로 있으며, 각 타임스탬프에는 해당 시점의 쿼리가 바로 그 쿼리인지 여부가 1 또는 0으로 표기되어 있다. 저~ 위의 예에서, q2의 스트림은 (0, 1, 0, 0, 1, 1, 0)으로 표현될 것이다. (좀더 일반화하면 타임스탬프마다 그 쿼리가 유입된 횟수가 적혀있다고 해도 된다. 단위 시간 당 유입량) 그랬을 때, 마지막 k개의 타임스탬프 내에서 1이 몇 개인지 세는 문제다. 가령, 어제 하루 동안 이 쿼리가 들어온 횟수는? 지난 일주일은? 최근 15일은? 이렇게 임의의 k를 얘기했을 때 거의 바로 대답할 수 있어야 한다. 이 문제는 지금까지와는 달리 좀더 복잡한 자료구조를 도입해야 하며, 이를 위해 Datar-Gionis-Indyk-Motwani, 줄여서 DGIM 알고리즘이 제안되었다.

6. Decaying Windows

마지막이다. 5번에서는 k의 값을 지정했었는데, 그러면 최근 k개 데이터는 똑같은 가중치로 반영되고, k+1번째 데이터부터는 그냥 버려진다. 이보다 조금 더 부드럽게(smooth) 셀 수는 없을까? 물론, 가능하다. 아래 그림에서 직사각형의 Sliding Window 대신 곡선 함수를 이용해서 오래된 데이터의 가중치는 낮추면 된다. 계산 효율이 좋을 뿐 아니라 최근 데이터가 없는 지나치게 낡은 데이터를 걸러내기도 용이하다는 게 장점이다.

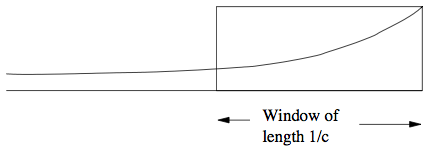
이상, Mining of Massive Datasets 4장에서 해결하려고 하는 문제들을 정리해봤다. 구체적인 내용은 책을 읽어보자.