펀드 평가 방법: 위험조정 수익률 지수
이 글에 앞서 펀드 평가 방법: 베타β와 젠센의 알파α를 읽으면 도움이 된다.
젠센의 알파를 통해서 특정 펀드(=포트폴리오)가 벤치마크 대비 얼마나 높은 수익을 거두었는지 알 수 있다. 이 말인즉슨 알파 값에 따라서 펀드 운용 성과의 순위를 매길 수 있다는 뜻이다. 펀드가 감수한 위험을 고려해 그 수익률을 평가하는 척도는 이미 여러 개 나와 있다. 모두가 약속이나 한 듯이 비율(Ratio)이라는 단어를 달고 있는데, 기본적으로 ‘수익 나누기 위험’의 꼴을 따르기 때문이다. 감수한 위험의 크기에 따라 수익률을 조정하기 때문에 이들을 위험조정 수익률(Risk-adjusted Return)이라고 부른다. 그리고 당연히 이 값들이 클수록 좋은 펀드라고 볼 수 있다.
Treynor Ratio
잭 트레이너(Jack L. Treynor)가 개발한 척도(measure)로서, 수익률-변동성 비율(reward-to-volatiliry ratio)이라고도 한다. 여기서 중요한 것은 트레이너의 스펠링이 Trainer가 아니라는 점이다. 무위험 수익 대비 초과 수익을 포트폴리오의 베타로 나누면 된다.
\[T=\frac{E[R_{p}-R_{f}]}{\beta_{p}}\]시장(벤치마크 지수) 자체를 대상으로 계산하면, 시장의 베타는 1이므로 Treynor Ratio는 Rp - Rf이다. (Rp는 포트폴리오 수익률, Rf는 무위험 수익률)
Sharpe Ratio
1990년, 그의 스승 해리 마코위츠(Harry Markowitz)와 함께 노벨경제학상을 수상한 윌리엄 샤프(William Forsyth Sharpe)가 개발한 지수이다. Treynor Ratio와 비슷한데, Sharpe Ratio는 수익을 베타 대신 포트폴리오의 표준편차로 나눈다는 점이 다르다.
\[S=\frac{E[R_{p}-R_{f}]}{\sqrt{var[R-R_{f}]}}\]표준편차를 구할 때 1년 단위의 가격 변동을 쓰느냐 아니면 3개월 혹은 3년 단위의 변동을 쓰느냐에 따라서 결과 값이 많이 달라질 수 있음을 기억하자.
Information Ratio
젠센의 알파를 설명하면서 어떤 펀드매니저가 연달아 높은 알파를 기록하면 그의 안목을 신뢰해도 될까라는 질문들 던졌었다. 그에 대한 답을 Information Ratio로 찾아보자. 앞서 설명한 지수들은 분자에 무위험 수익률 대비 펀드 수익이 자리하고 있었다. 하지만, Information Ratio에서는 벤치마크 대비 수익, 즉 알파의 평균이 그 자리를 대체했다. 펀드의 성과를 훨씬 엄격하게 벤치마크 지수와 비교하겠다는 의미다. 게다가 분모에는 이 알파의 표준펀차(Tracking Error)가 들어온다. 얼마나 일관적으로 초과수익을 달성했는지 따지겠다는 거다.
\[IR = \frac{E[R-R_{b}]}{\sqrt{var[R-R_{b}]}}\]BM 대비 초과수익이 너무 들쭉날쭉해도 안 되고, 평균적인 초과수익은 높아야 하니, 펀드매니저 입장에서는 무척 혹독한 평가 척도가 아닐까 싶다. (그런데도 모든 난관을 극복하고 높은 점수를 기록하는 펀드가 있다면…?)
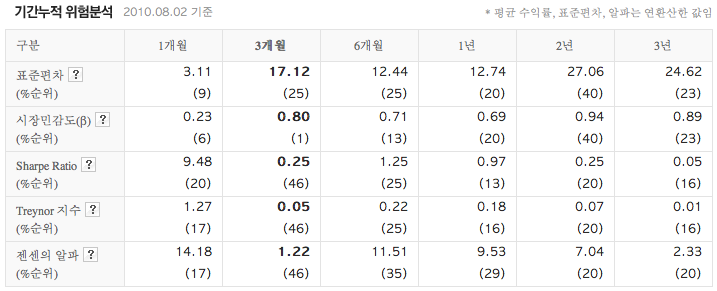
드디어 펀드 평가서에 나오는 암호 같은 각종 지수의 의미를 이해하게 되었다.