지난 글에 이어서 선형 회귀분석을 이용해 경제 변수 사이의 관계를 분석하고 있다. 그런데 변수 값의 변화량이 동일하다고 해도 그것이 갖는 의미와 효과는 상황에 따라 다를 수 있다. 가령 소득과 삶의 만족도의 관계를 연구할 때 원래 소득이 100만원일 때와 1000만원일 때 100만원의 증가를 동일하게 취급해도 될까? 안 된다면 어떻게 해야 할까?

쉽게 생각할 수 있는 방법은 변화의 절대량이 아니라 변화의 비율에 대한 효과를 추정하는 것이다. 즉 소득이 10% 증가하면 만족도는 어떻게 바뀌는가. 적용 방법은 간단하다. 변수에 로그를 취하면 된다.

만족도 = b0 + b1·log(소득)

이 모델이 적합하다고 했을 때, 소득이 p% 증가했을 때 만족도가 얼마나 변하는지 보자.

원래만족도 = b0 + b1·log(소득)
증가후만족도 = b0 + b1·log(소득·(1+p))
만족도 변화 = 증가후만족도 - 원래만족도 = b1·log(1+p)

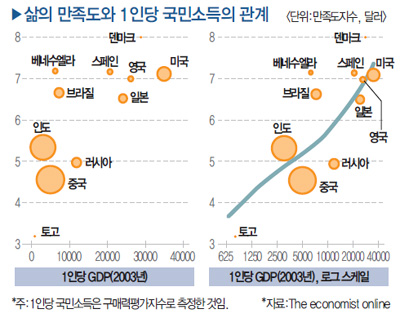
소득이 10% 증가할 때마다 삶의 만족도는 \(\log(1.1) \cdot b_1\) 만큼씩 증가한다. 찾아보니 원출처를 이코노미스트로 밝힌 매경의 기사에 관련된 그래프가 있었다. 왼쪽은 1인당 GDP를 그대로 썼을 때이고 오른쪽은 로그를 취했을 때인데, 차이를 확인할 수 있다.

꼭 독립변수에만 로그를 취할 이유는 없다. 종속변수에 로그를 씌워서 \(\log(y) = b_0 + b_1 \cdot x\)로 모델링했다면 x가 1단위 증가할 때 y는 \(\exp(b_1)-1\)퍼센트 증가한다고 해석할 수 있다. (e.g. 교육을 1년 더 받으면 연봉은 몇 퍼센트 증가하는가) 독립변수 x와 종속변수 y에 모두 로그를 취했다면 x가 p% 증가할 때 y는 \(\exp(1+p)^{b}-1\)퍼센트 증가한다는 의미가 된다.

이 방법은 결국 변수의 현재값에 따라서 단위 변화가 갖는 효과의 크기가 달라지게 하는 것이다. \(y = b_0 + b_1 \cdot \log(x)\)를 미분하면 dy/dx = 1/x 이고, x가 커질수록 기울기는 완만해지며 단위 변화에 대한 y의 변화가 줄어든다. 소득을 10% 올리려면 100만원일 때는 10만원만 더 벌면 되지만 1000만원일 때는 100만원이나 더 벌어야 한다.

dy/dx를 조절하는 방법은 다양하다. 만약 x의 절대값이 클수록 단위 변화에 더 민감하게 만들고 싶다면 \(y = b_0 + b_1 \cdot x^2\)으로 모델링할 수도 있다. (dy/dx = 2x) 만약 x의 1차항과 2차항을 동시에 포함하면 어떻게 될까?

이중에서 특히 b1과 b2의 부호가 다른 경우(b1 > 0, b2 < 0)를 생각해보자. \(- b_1 / (2 \cdot b_2)\)보다 작은 동안에는 x가 커질수록 y에 플러스로 작용한다. 하지만 증가하는 정도가 조금씩 줄어들다가 \(- b_1 / (2 \cdot b_2)\)를 지나면 이제부터는 x가 증가할수록 y는 감소하게 된다. (어떤 경우에 이런 관계가 나올까?)

독립변수 x1의 효과가 다른 독립변수 x2의 값에 따라 다를 수 있다. 소득과 만족도의 관계에서 성별에 따라서 소득이 끼치는 영향이 다른지 분석하려면 어떻게 해야 할까? “여성”이라는 변수를 만들고, 여성일 때는 1 아닐 때는 0이라는 값을 준다. 이 “여성” 변수와 “log(여성)”을 곱한 상호작용항(Interaction Term)을 추가한다.

만족도 = b0 + b1·log(소득) + b2·여성·log(소득)

편의상 위의 식을 log(소득)으로 미분하면, (b1 + b2·여성)이 나온다. 소득이 만족도에 주는 영향이 여성에게서 더 크다면 b2가 양수가 되고, 성별에 따른 차이가 없다면 b2는 0이 된다. 학업성취도 요인을 분석할 때 공부한 시간과 그 과목에 대한 흥미도의 상호작용항을 추가하면 흥미도에 따른 공부 시간의 효과를 추정할 수 있고 현재 필요한 게 무엇인지 좀더 정확한 진단을 내릴 수 있을 것이다.

보다 현실적인 모델을 만들기 위해 변수에 적당한 함수를 적용하거나 관계있는 변수를 결합하는 방법을 살펴보았다.

참고자료

• Jeffrey M. Wooldridge, 박상수 역, 『계량경제학 1』, 박영사, 2015