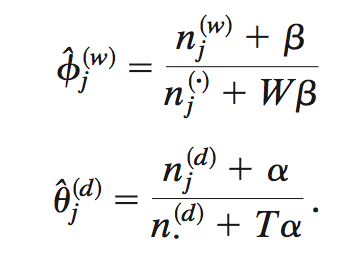LDA 파라미터 추정: 깁스 샘플링을 써서
이런 걸 써봐야 누가 읽겠어 했던 글이 의외로 블로그의 트래픽을 먹여살리고 있다. 4년 전에 쓴 LDA(Latent Dirichlet Allocation): 겉핥기는 지금까지도 꾸준히 조회수 탑을 달리는 스테디포스트가 되었다. 이제와서 보니 허술한 구석이 많은데, 특히 파라미터 추정을 대충 넘어간 것 같아서 좀더 자세히 적어본다.
LDA에서 모델 파라미터를 추정하는 방법은 크게 2가지가 있다. Blei 교수의 원논문에 나오는 Variational Inference가 있고, 깁스 샘플링(Gibbs Sampling) 방식이 있는데, 이글에서는 이해하기 쉽고 수식을 해석하기도 용이한 깁스 샘플링 쪽을 설명한다. (사실 Variational Inference는 아직 잘 모르겠다.)
이 글을 보면, LDA의 개념도 잘 설명되어 있고, 문서에 출현한 특정 단어의 토픽을 추정하는 수식이 나온다.
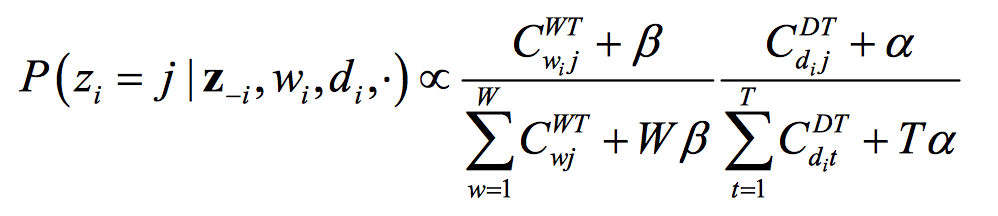
이를 말로 풀어보면, 문서 집합에서 i번째에 나오는 단어 w의 토픽이 j일 확률은 다음의 두 가지에 영향을 받는다는 것이다.
- 요소1: 토픽 j에 할당된 전체 단어 중에서 해당 단어의 점유율이 높을수록 j일 확률이 크다.
- 요소2: i가 속한 문서 내 다른 단어가 토픽 j에 많이 할당되었을수록 j일 확률이 크다. 문서에 단어가 10개가 있는데, 현재 보고 있는 것을 제외하고, 7개가 j1에 할당되었고, 2개가 j2에 할당되었다면, w의 토픽은 j1일 확률이 더 크다.
의미가 그럴듯하게 해석되는 수식이다. 요소2에 의해서, 한 문서에 같이 등장하는 빈도가 큰 단어들은 같은 토픽으로 묶일 것이다. 하지만 대부분의 단어가 몇 개의 거대한 토픽으로 쏠리는 것은 요소1에 의해서 방지된다. 토픽에 할당된 유니크 단어가 많아질수록 단어를 잡아당기는 힘이 약해지고, 반면에 할당된 단어가 얼마 없는 토픽은 강하게 새로운 단어를 끌어당긴다. 그 결과, 서로 관련이 있는 단어들끼리 적당한 크기의 토픽으로 클러스터링 된다.
LDA 모델로부터 어떻게 이런 수식이 나오는 걸까? 위 논문 저자들이 쓴 Finding scientific topics에 전체 과정이 잘 설명되어 있다.
\(P(\vec{z}, \vec{w})\)를 구하자
우리가 알고 싶은 것은 \(P(\vec{z} \lvert \vec{w})\)이다. 여기서 \(\vec{w}\)와 \(\vec{z}\)는 벡터이고, \(w_{i}\)와 \(z_{i}\)는 전체 문서셋에서 i번째 단어와 토픽을 의미한다. 전체 토큰의 개수는 N이므로, \(\vec{w}\)와 \(\vec{z}\) 벡터의 크기는 N이다. \(P(\vec{z} \lvert \vec{w})\)를 알고 나면, 개별 문서의 주제 벡터 \(\theta_{d}\)와 주제가 j일 때 단어 w가 생성될 확률 \(P(w \lvert z=j) = \phi_{j}^{(w)}\)도 구할 수 있다.
베이즈룰(Bayes Rule)에 의해서,
\[P(\vec{z} \vert \vec{w}) = \frac{P(\vec{w} \vert \vec{z}) \times P(\vec{z})}{P(\vec{w})}\]우선 분자에 나오는 \(P(\vec{z})\)를 계산해보자. LDA의 확률 모델에 따르면, z는 문서의 토픽 분포인 \(\theta\)로부터 생성된다.
\[P(\vec{z}) = \int P(\vec{z} \vert \theta)P(\theta)d\theta\]\(\theta\)는 파라미터가 \(\alpha\)인 디리클레 분포를 따른다고 했으므로
\[P(\vec{z}) = \int P(\vec{z} \vert \theta)P(\theta \vert \alpha)d\theta\]이 식은 우리가 지정하는 하이퍼 파라미터 \(\alpha\)가 \(\vec{z}\)의 생성에 어떻게 관여하는지 보여준다. \(\theta\)는 파라미터가 \(\alpha\)인 디리클레 분포에서 나오고, \(\vec{z}\)는 파라미터가 그 \(\theta\)인 다항 분포(Multinomial Distribution)를 따른다. 여기서는 단순화를 위해 \(\alpha\)를 Symmetric Dirichlet Prior라고 가정하고 있다.
문서끼리는 서로 독립이므로
\[P(\vec{z}) = \prod_{d=1}^D \int P(\vec{z} \vert \theta_{d})P(\theta_{d} \vert \alpha)d\theta_{d}\]D는 전체 문서의 개수이고, \(\theta_{d}\)는 문서 d의 토픽 벡터다. 여기서 \(\theta_{d}\)로 적분해버리면(Integral out)
\[P(\vec{z}) = \prod_{d=1}^D \frac{\Gamma(T\alpha)}{\Gamma(\alpha)^T} \frac{\prod_j \Gamma(n_{j}^{(d)}+\alpha)}{\Gamma(n^{(d)}+T\alpha)} = \big(\frac{\Gamma(T\alpha)}{\Gamma(\alpha)^T}\big)^{D} \prod_{d=1}^D \frac{\prod_j \Gamma(n_{j}^{(d)}+\alpha)}{\Gamma(n^{(d)}+T\alpha)}\]\(P(\vec{z})\)를 직접 계산할 수 있게 된다. \(n^{(d)}\)는 문서 d의 전체 토큰 개수, \(n_{j}^{(d)}\)는 문서 d에서 토픽 j로 할당된 토큰 개수이다. 감마 함수는 일단 간단하게
\[\Gamma(n) = (n-1)!\]로 생각하고 넘어가자.
\(P(\vec{z})\)와 같은 방식으로 \(P(\vec{w} \lvert \vec{z})\)도 \(\phi\)로 적분하면,
\[P(\vec{w} \vert \vec{z}) = \big(\frac{\Gamma(W\beta)}{\Gamma(\beta)^W}\big)^{T} \prod_{j=1}^{T} \frac{\prod_w \Gamma({n_{j}}^{(w)}+\beta)}{\Gamma(n_{j}+W\beta)}\]가 된다. 이렇게 나온 \(P(\vec{w} \lvert \vec{z})\)와 \(P(\vec{z})\)를 해석하면, 결합 분포(Joint Distribution) \(P(\vec{z}, \vec{w})\)가 실제로 서두에서 얘기한 두 요소에 비례한다는 것을 확인할 수 있다. 그리고 LDA에서 디리클레 분포를 사전확률(Prior Probability)로 쓰는 것이 실제로 어떤 의미를 갖는지도 알 수 있다. \(z_{i}\)를 추정할 때, 그 문서 내에서 토픽 j로 할당된 단어가 하나도 없더라도, \(P(z_{i}=j)\) 값이 0이 아니다. 마찬가지로, 단어 w가 토픽 j로 할당된 적이 한 번도 없었더라도 여전히 가능성의 여지를 남겨두는 스무딩(Smoothing) 역할을 한다. (만약 Symmetric Prior가 아니었다면, 특정 토픽으로 할당될 확률을 높여주는 역할도 하게 된다.)
깁스 샘플링이 필요한 이유
복잡한 수식을 풀었으니 이제 다 끝난 것 같지만, 아직 문제가 남았다. 우리가 알고 싶은 것은 \(P(\vec{z} \lvert \vec{w})\)라는 사후확률분포(Posterior Probability Distribution)인데, 위의 방법을 쓰면 분자는 풀리지만, 분모인 \(P(\vec{w})\)는 여전히 계산할 수 없다. 게다가 \(P(\vec{z} \lvert \vec{w})\)에서 \(\vec{z}\)의 가능한 조합 개수는 \(T^{N}\)개나 된다. 이 확률분포를 얻으려면 어떻게 해야 할까?
만약 “어떤 방법”을 써서, 미지의 \(P(\vec{z} \lvert \vec{w})\) 분포로부터 “샘플”들을 뽑아낼 수 있으면 어떨까? 그러면 -랜덤으로 100명의 키를 재서 한국인의 평균키를 추정하듯이- 미지의 분포도 추정할 수 있지 않을까? 바로 그걸 하는 게 깁스 샘플링이다. (깁스 샘플링에 대해서는 이 글도 같이 참고하면 도움이 될 것 같다.)
그럼 깁스 샘플링은 어떻게 알지도 못하는 분포에서 샘플을 뽑는가? 논문에서는 목표분포(Target Distribution)에 수렴하도록 마코프 체인을 만들고, 그로부터 샘플을 얻는다고 원리를 설명한다. (이런 방식을 MCMC라고 한다.)
In Markov chain Monte Carlo, a Markov chain is constructed to converge to the target distribution, and samples are then taken from that Markov chain. (Finding scientific topics)
복잡해 보이지만, 실제로 계산하는 방법은 어렵지 않다. 알고 싶은 결합 분포의 랜덤변수 값 \(z_{i}\)를 추정할 때, 그 \(z_{i}\)를 제외한 다른 모든 변수(\(z_{-i}\)라고 표기한다)는 현재 할당된 값으로 고정되어 있다고 가정하고, \(z_{i}\) 값을 샘플링하는 것이다. z에 영향을 주는 요소는 이미 위에서 계산해 놓았으니, 이를 이용하면
\[P(z_{i}=j \vert \vec{z}_{-i}, \vec{w}) \propto \frac{n_{-i, j}^{(w_{i})}+\beta}{n_{-i,j}+W\beta} \frac{n_{-i,j}^{d_{i}}+\alpha}{n_{-i}^{d_{i}}+T\alpha}\]\(z_{1}\)부터 \(z_{N}\)까지 쭉 돌면서 \(\vec{z}\)의 값을 채우면, 그게 하나의 깁스 샘플이 된다. 이 상태에서 다시 \(z_{1}\) ~ \(z_{N}\)을 돌면 두 번째 샘플을 얻을 수 있고, 이 과정을 계속 반복하면 된다. 초기값을 랜덤으로 생성하더라도 충분히 많은 수의 반복을 하고 난 뒤에 얻는 샘플은 목표분포를 따른다고 하므로 이를 통해 \(\vec{z}\)를 추정할 수 있다.
\(P(\vec{z} \lvert \vec{w})\)를 얻고 나면, 이제 진짜 마지막으로, 토픽 j에서 단어 w가 나올 확률 \(\phi_{j}^{(w)}\)와 문서 d의 주제 벡터 \(\theta_{d}\)를 다음과 같이 구할 수 있다.